ГИПЕРБОЛОИД

ГИПЕРБОЛО́ИД (гипербола ж-а гр. tidos – форма, көрүнүш) – туюк эмес борбордук экинчи тартиптеги бет. Гиперболоиддин эки түрү – бир көӊдөйлүү (1-чийме) ж-а эки көӊдөйлүү (2-чийме) бар. Гиперболоид кандайдыр бир тегиздик м-н кесилишкенде экинчи тартиптеги түрдүү ийрилерди (эллипс, гипербола, парабола ж. б.) пайда кылат. Гиперболоиддин канондук теӊдемелери: ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=1$ – бир өӊдөйлүү гиперболоид; ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=-1$ – эки көӊдөйлүү гиперболоид, мында $a,\ b$ ж-а с сандары гиперболоиддин жарым октору деп аталат. Гиперболоид $Oz$ огу аркылуу өткөн тегиздик м-н кесилишкенде гипербола, Оz огуна перпендикуляр тегиздик м-н кесилишкенде эллипс пайда болот. Гиперболоиддин симметриялуу үч тегиздиги бар. Гиперболоид ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=0$ теӊдемеси м-н аныкталуучу конус асимптоталык конус деп аталат. Эгерде $a=b=c$ болсо, т у у р а гиперболоидди, эки

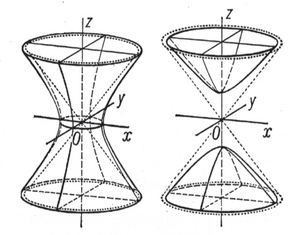
1-чийме. 2-чийме.
жарым огу барабар болсо, а й л а н м агиперболоидди берет. Бир көӊдөйлүү гиперболоид сызыктуу бетке ээ, к. Бир көӊдөйлүү гиперболоид,