ВЕКТОРДУК ЭСЕПТӨӨ –: нускалардын айырмасы
м (1 версия) |
vol2_>KadyrM No edit summary |
||
| 1 сап: | 1 сап: | ||
'''ВЕКТОРДУК ЭСЕПТӨӨ – ''' математиканын евклид мейкиндигиндеги векторлорду ж-а алар м-н болгон амалдарды изилдөөчү бөлүмү. В. э. 19-к-дын орто ченинен баштап механика ж-а физикада коюлган талаптарга жараша өнүккөн. Англ. математик У. Гамильтон ж-а нем. математиги Г. Грассмандын (1844–50) гиперкомплекстик сандарды изилдөөлөрү В. э-гө негиз салган. Алардын идеяларын англ. физик К. Максвелл электр ж-а магнит ж-дөгү эмгектеринде пайдаланган. Амер. физик Ж. Гиббс В. э-нү азыркы деӊгээлине жеткирген. В. э-нүн өсүшүнө орус математиктери М. В. Остроградский, А. П. Котельников ж-а сов. илимпоздор Д. Н. Зейлигер, П. А. Широков ж. б. чоӊ салым кошушкан. В. э. вектордук алгебра ж-а вектордук | |||
анализ болуп бөлүнөт. | <br/>анализ болуп бөлүнөт. | ||
==Вектордук алгебра – ==<br> | <br/> | ||
векторлор м-н жүргүзүлгөн эӊ жөнөкөй амалдарды окутуп-үйрөтүүчү ''вектордук эсептөөнүн'' бир бөлүмү. Алар векторлор м-н жүргүзүлгөн с ы з ы к т у у а м а л д а р: векторлорду кошуу ж-а векторду санга көбөйтүү. '''''а'' '''векторунун башталышынан '''''b'' '''векторунун аягына жүргүзүлгөн вектор '''''а'' '''ж-а '''''b'' '''векторлорунун с у м м а с ы '''''а+b'' '''деп аталат (эгер '''''а'''''нын аягы м-н '''''b'''''нын башталышы дал келишсе). Векторлорду кошуунун төмөнкүдөй касиеттери бар: '''''а+b=b+а'' '''(коммутативдик), ('''''а+b)+с=а+(b+с''''') (ассоциативдик), '''''а''+0=''а'' '''(нөлдүк элементтин болушу), '''''а+(–а'')=0 '''(карама-каршы элементтин болушу), мында '''0 '''– нөлдүк вектор, '''–''а'' '''вектору '''''а'' '''векторуна карама-каршы вектор. '''''х+b=а'' '''барабардыгын канааттандырган '''''х'' '''вектору '''''а'' '''ж-а '''''b'' '''векторлорунун '''''а–b'' '''айырмасы деп аталат. Модулу '''''а''''' болгон (эгер >0 болсо, багыты '''''а'''''нын багытына дал келген ж-а <0ж-а багыты '''''а'''''нын багытына карама-каршы багытталган) вектор '''''а (а''0) '''векторунун 0)санына болгон көбөйт үндүсү '''''а'' '''деп аталат. Эгер 0 же (ж-а) '''''а''=0 '''болсо, анда '''''а''=0 '''болот. Векторлорду санга көбөйтүү төмөнкү касиеттерге ээ: ('''''а+b)=а+b'' '''(векторлорду кошууга карата дистрибутивдик), (+)'''''а=а+а'' '''(сандарды кошууга карата дистрибутивдик), ('''''а)=()а'' '''(ассоциативдик), 1·'''''а=а'' '''(1ге көбөйтүү). Мейкиндиктеги бардык векторлордун көптүгүн (киргизилген ж-а жогорудагы аксиомаларга баш ийген векторлорду кошуу ж-а санга көбөйтүү операциялары м-н бирдикте) ''вектордук мейкиндик'' деп айтылат. | ==Вектордук алгебра – == | ||
==Вектордук анализ, ==<br> | <br/>векторлор м-н жүргүзүлгөн эӊ жөнөкөй амалдарды окутуп-үйрөтүүчү ''вектордук эсептөөнүн'' бир бөлүмү. Алар векторлор м-н жүргүзүлгөн с ы з ы к т у у а м а л д а р: векторлорду кошуу ж-а векторду санга көбөйтүү. '''''а'' '''векторунун башталышынан '''''b'' '''векторунун аягына жүргүзүлгөн вектор '''''а'' '''ж-а '''''b'' '''векторлорунун с у м м а с ы '''''а+b'' '''деп аталат (эгер '''''а'''''нын аягы м-н '''''b'''''нын башталышы дал келишсе). Векторлорду кошуунун төмөнкүдөй касиеттери бар: '''''а+b=b+а'' '''(коммутативдик), ('''''а+b)+с=а+(b+с''''') (ассоциативдик), '''''а''+0=''а'' '''(нөлдүк элементтин болушу), '''''а+(–а'')=0 '''(карама-каршы элементтин болушу), мында '''0 '''– нөлдүк вектор, '''–''а'' '''вектору '''''а'' '''векторуна карама-каршы вектор. '''''х+b=а'' '''барабардыгын канааттандырган '''''х'' '''вектору '''''а'' '''ж-а '''''b'' '''векторлорунун '''''а–b'' '''айырмасы деп аталат. Модулу '''''а''''' болгон (эгер >0 болсо, багыты '''''а'''''нын багытына дал келген ж-а <0ж-а багыты '''''а'''''нын багытына карама-каршы багытталган) вектор '''''а (а''0) '''векторунун 0)санына болгон көбөйт үндүсү '''''а'' '''деп аталат. Эгер 0 же (ж-а) '''''а''=0 '''болсо, анда '''''а''=0 '''болот. Векторлорду санга көбөйтүү төмөнкү касиеттерге ээ: ('''''а+b)=а+b'' '''(векторлорду кошууга карата дистрибутивдик), (+)'''''а=а+а'' '''(сандарды кошууга карата дистрибутивдик), ('''''а)=()а'' '''(ассоциативдик), 1·'''''а=а'' '''(1ге көбөйтүү). Мейкиндиктеги бардык векторлордун көптүгүн (киргизилген ж-а жогорудагы аксиомаларга баш ийген векторлорду кошуу ж-а санга көбөйтүү операциялары м-н бирдикте) ''вектордук мейкиндик'' деп айтылат. | ||
в е к т о р д у к т а л д о о – вектордук эсептөөлөрдүн бир бөлүмү. Ал вектордук ж-а скалярдык талааларды, векторлордун матем. касиеттерин үйрөтөт. Мында ''математикалык анализдин'' каражаттары м-н бир же көп аргументтү вектордук ж-а скалярдык функциялар изилденет. Эгер {t} көптүгүндөгү t өзгөрмөсүнүн ар бир маанисине белгилүү бир закон б-ча r вектору туура келсе, анда {t} көптүгүндө r = r (t) вектор-функциясы берилген деп эсептелет. 3 өлчөмдүү мейкиндикте r = r (t) вектор- функциясынын берилиши ''x = x''(t), ''y = y(t), z = z(t'') үч скалярдык функциясынын берилишине эквиваленттүү. Координата башталышы – 0дөн чыккан r(t) векторлорунун учтарынын көптүгү г о д о г р а ф деп аталат. Эгер t аргументи убакыт катары алынса, анда r(t) вектор функциясы, r(t) функциясынын годографы L ийри сызыгынын М чекитиндеги кыймыл законун көрсөтөт. Вектор – функцияны үйрөтүүдө туунду түшүнүгү чоӊ роль аткарат ж-а төмөнкүчө киргизилет: эгер t аргументине t0 өсүндүсү берилсе ж-а r = r(t + t) – r(t) вектору (сүрөттө МР вектору) 1/tга көбөйтүлсө, анда t 0 болгондо dr/dt катышынын чеги (предели) r(t) вектор функциясынын т у у н д у с у деп аталат, ал r(t) же dr/dt аркылуу белгиленет. Бул туунду – L ийри сызыгынын (годографынын) М чекитинде жүргүзүлгөн жаныма. Эгер r(t) функциясы М чекитинин L ийри сызыгы боюнча чекиттин кыймыл закону деп каралса, анда r (t) туундусу ушул чекиттин кыймылынын ылдамдыгы болуп эсептелет. Вектор-функциялардын түрдү көбөйтүндүлөрүн эсептөө эрежелери кадимки функциялардыкына окшош: ('''r'''<sub>1</sub>, '''r'''<sub>2</sub>)=('''r'''<sub>1</sub>, '''r'''<sub>2</sub>)+ ('''r'''<sub>1</sub>, '''r'''<sub>2</sub>), ['''r'''<sub>1</sub>, '''r'''<sub>2</sub>]=['''r'''<sub>1</sub>, '''r'''<sub>2</sub>]+ ['''r'''<sub>1</sub>, '''r'''<sub>2</sub>]. Скалярдык | <br/> | ||
==Вектордук анализ, == | |||
<br/>в е к т о р д у к т а л д о о – вектордук эсептөөлөрдүн бир бөлүмү. Ал вектордук ж-а скалярдык талааларды, векторлордун матем. касиеттерин үйрөтөт. Мында ''математикалык анализдин'' каражаттары м-н бир же көп аргументтү вектордук ж-а скалярдык функциялар изилденет. Эгер {t} көптүгүндөгү t өзгөрмөсүнүн ар бир маанисине белгилүү бир закон б-ча r вектору туура келсе, анда {t} көптүгүндө r = r (t) вектор-функциясы берилген деп эсептелет. 3 өлчөмдүү мейкиндикте r = r (t) вектор- функциясынын берилиши ''x = x''(t), ''y = y(t), z = z(t'') үч скалярдык функциясынын берилишине эквиваленттүү. Координата башталышы – 0дөн чыккан r(t) векторлорунун учтарынын көптүгү г о д о г р а ф деп аталат. Эгер t аргументи убакыт катары алынса, анда r(t) вектор функциясы, r(t) функциясынын годографы L ийри сызыгынын М чекитиндеги кыймыл законун көрсөтөт. Вектор – функцияны үйрөтүүдө туунду түшүнүгү чоӊ роль аткарат ж-а төмөнкүчө киргизилет: эгер t аргументине t0 өсүндүсү берилсе ж-а r = r(t + t) – r(t) вектору (сүрөттө МР вектору) 1/tга көбөйтүлсө, анда t 0 болгондо dr/dt катышынын чеги (предели) r(t) вектор функциясынын т у у н д у с у деп аталат, ал r(t) же dr/dt аркылуу белгиленет. Бул туунду – L ийри сызыгынын (годографынын) М чекитинде жүргүзүлгөн жаныма. Эгер r(t) функциясы М чекитинин L ийри сызыгы боюнча чекиттин кыймыл закону деп каралса, анда r (t) туундусу ушул чекиттин кыймылынын ылдамдыгы болуп эсептелет. Вектор-функциялардын түрдү көбөйтүндүлөрүн эсептөө эрежелери кадимки функциялардыкына окшош: ('''r'''<sub>1</sub>, '''r'''<sub>2</sub>)=('''r'''<sub>1</sub>, '''r'''<sub>2</sub>)+ ('''r'''<sub>1</sub>, '''r'''<sub>2</sub>), ['''r'''<sub>1</sub>, '''r'''<sub>2</sub>]=['''r'''<sub>1</sub>, '''r'''<sub>2</sub>]+ ['''r'''<sub>1</sub>, '''r'''<sub>2</sub>]. Скалярдык | |||
<br/> | |||
[[File:ВЕКТОРДУК ЭСЕПТӨӨ –67.png | thumb | none]] | |||
талааны окуп-үйрөнүүнүн негизги түшүнүктөрүнүн бири болуп градиент эсептелет. Вектордук анализдин негизги дифференциалдык амалдары – ''градиент, дивергенция'' ж-а куюн (ротор). В. а-ди амер. физик Ж. Гиббс киргизген. Орус окумуштуусу М. В. Остроградский анын негизги теоремасын далилдеген. Англ. физик О. Хевисайд В. а-ди өз эмгектеринде 1882-жылдан тартып колдоно баштаган. 1907-ж. орус математиги П. О. Сомовдун «Вектордук анализ» деген китеби жарык көргөн. | талааны окуп-үйрөнүүнүн негизги түшүнүктөрүнүн бири болуп градиент эсептелет. Вектордук анализдин негизги дифференциалдык амалдары – ''градиент, дивергенция'' ж-а куюн (ротор). В. а-ди амер. физик Ж. Гиббс киргизген. Орус окумуштуусу М. В. Остроградский анын негизги теоремасын далилдеген. Англ. физик О. Хевисайд В. а-ди өз эмгектеринде 1882-жылдан тартып колдоно баштаган. 1907-ж. орус математиги П. О. Сомовдун «Вектордук анализ» деген китеби жарык көргөн. | ||
''Ад.: Александров П. С.'' Лекции по аналитической геометрии. М., 1968; ''Ефимов Н. В.'' Краткий курс аналитической геометрии. 9-ое изд. М., 1967. | <br/>''Ад.: Александров П. С.'' Лекции по аналитической геометрии. М., 1968; ''Ефимов Н. В.'' Краткий курс аналитической геометрии. 9-ое изд. М., 1967. | ||
''А. А. Чекеев, С. С. Токсонбаев.'' | <br/>''А. А. Чекеев, С. С. Токсонбаев.'' | ||
[[Category: 2-том]] | [[Category: 2-том]] | ||
02:40, 25 Март (Жалган куран) 2024 -деги абалы
ВЕКТОРДУК ЭСЕПТӨӨ – математиканын евклид мейкиндигиндеги векторлорду ж-а алар м-н болгон амалдарды изилдөөчү бөлүмү. В. э. 19-к-дын орто ченинен баштап механика ж-а физикада коюлган талаптарга жараша өнүккөн. Англ. математик У. Гамильтон ж-а нем. математиги Г. Грассмандын (1844–50) гиперкомплекстик сандарды изилдөөлөрү В. э-гө негиз салган. Алардын идеяларын англ. физик К. Максвелл электр ж-а магнит ж-дөгү эмгектеринде пайдаланган. Амер. физик Ж. Гиббс В. э-нү азыркы деӊгээлине жеткирген. В. э-нүн өсүшүнө орус математиктери М. В. Остроградский, А. П. Котельников ж-а сов. илимпоздор Д. Н. Зейлигер, П. А. Широков ж. б. чоӊ салым кошушкан. В. э. вектордук алгебра ж-а вектордук
анализ болуп бөлүнөт.
Вектордук алгебра –
векторлор м-н жүргүзүлгөн эӊ жөнөкөй амалдарды окутуп-үйрөтүүчү вектордук эсептөөнүн бир бөлүмү. Алар векторлор м-н жүргүзүлгөн с ы з ы к т у у а м а л д а р: векторлорду кошуу ж-а векторду санга көбөйтүү. а векторунун башталышынан b векторунун аягына жүргүзүлгөн вектор а ж-а b векторлорунун с у м м а с ы а+b деп аталат (эгер анын аягы м-н bнын башталышы дал келишсе). Векторлорду кошуунун төмөнкүдөй касиеттери бар: а+b=b+а (коммутативдик), (а+b)+с=а+(b+с) (ассоциативдик), а+0=а (нөлдүк элементтин болушу), а+(–а)=0 (карама-каршы элементтин болушу), мында 0 – нөлдүк вектор, –а вектору а векторуна карама-каршы вектор. х+b=а барабардыгын канааттандырган х вектору а ж-а b векторлорунун а–b айырмасы деп аталат. Модулу а болгон (эгер >0 болсо, багыты анын багытына дал келген ж-а <0ж-а багыты анын багытына карама-каршы багытталган) вектор а (а0) векторунун 0)санына болгон көбөйт үндүсү а деп аталат. Эгер 0 же (ж-а) а=0 болсо, анда а=0 болот. Векторлорду санга көбөйтүү төмөнкү касиеттерге ээ: (а+b)=а+b (векторлорду кошууга карата дистрибутивдик), (+)а=а+а (сандарды кошууга карата дистрибутивдик), (а)=()а (ассоциативдик), 1·а=а (1ге көбөйтүү). Мейкиндиктеги бардык векторлордун көптүгүн (киргизилген ж-а жогорудагы аксиомаларга баш ийген векторлорду кошуу ж-а санга көбөйтүү операциялары м-н бирдикте) вектордук мейкиндик деп айтылат.
Вектордук анализ,
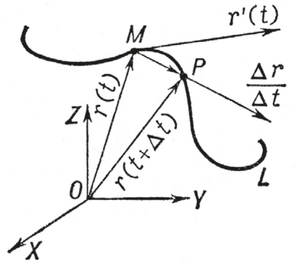
в е к т о р д у к т а л д о о – вектордук эсептөөлөрдүн бир бөлүмү. Ал вектордук ж-а скалярдык талааларды, векторлордун матем. касиеттерин үйрөтөт. Мында математикалык анализдин каражаттары м-н бир же көп аргументтү вектордук ж-а скалярдык функциялар изилденет. Эгер {t} көптүгүндөгү t өзгөрмөсүнүн ар бир маанисине белгилүү бир закон б-ча r вектору туура келсе, анда {t} көптүгүндө r = r (t) вектор-функциясы берилген деп эсептелет. 3 өлчөмдүү мейкиндикте r = r (t) вектор- функциясынын берилиши x = x(t), y = y(t), z = z(t) үч скалярдык функциясынын берилишине эквиваленттүү. Координата башталышы – 0дөн чыккан r(t) векторлорунун учтарынын көптүгү г о д о г р а ф деп аталат. Эгер t аргументи убакыт катары алынса, анда r(t) вектор функциясы, r(t) функциясынын годографы L ийри сызыгынын М чекитиндеги кыймыл законун көрсөтөт. Вектор – функцияны үйрөтүүдө туунду түшүнүгү чоӊ роль аткарат ж-а төмөнкүчө киргизилет: эгер t аргументине t0 өсүндүсү берилсе ж-а r = r(t + t) – r(t) вектору (сүрөттө МР вектору) 1/tга көбөйтүлсө, анда t 0 болгондо dr/dt катышынын чеги (предели) r(t) вектор функциясынын т у у н д у с у деп аталат, ал r(t) же dr/dt аркылуу белгиленет. Бул туунду – L ийри сызыгынын (годографынын) М чекитинде жүргүзүлгөн жаныма. Эгер r(t) функциясы М чекитинин L ийри сызыгы боюнча чекиттин кыймыл закону деп каралса, анда r (t) туундусу ушул чекиттин кыймылынын ылдамдыгы болуп эсептелет. Вектор-функциялардын түрдү көбөйтүндүлөрүн эсептөө эрежелери кадимки функциялардыкына окшош: (r1, r2)=(r1, r2)+ (r1, r2), [r1, r2]=[r1, r2]+ [r1, r2]. Скалярдык
талааны окуп-үйрөнүүнүн негизги түшүнүктөрүнүн бири болуп градиент эсептелет. Вектордук анализдин негизги дифференциалдык амалдары – градиент, дивергенция ж-а куюн (ротор). В. а-ди амер. физик Ж. Гиббс киргизген. Орус окумуштуусу М. В. Остроградский анын негизги теоремасын далилдеген. Англ. физик О. Хевисайд В. а-ди өз эмгектеринде 1882-жылдан тартып колдоно баштаган. 1907-ж. орус математиги П. О. Сомовдун «Вектордук анализ» деген китеби жарык көргөн.
Ад.: Александров П. С. Лекции по аналитической геометрии. М., 1968; Ефимов Н. В. Краткий курс аналитической геометрии. 9-ое изд. М., 1967.
А. А. Чекеев, С. С. Токсонбаев.