ВЕКТОРДУК ЭСЕПТӨӨ –: нускалардын айырмасы
No edit summary |
No edit summary |
||
| 5 сап: | 5 сап: | ||
<br/>векторлор м-н жүргүзүлгөн эӊ жөнөкөй амалдарды окутуп-үйрөтүүчү ''вектордук эсептөөнүн'' бир бөлүмү. Алар векторлор м-н жүргүзүлгөн с ы з ы к т у у а м а л д а р: векторлорду кошуу ж-а векторду санга көбөйтүү. <math>a</math> векторунун башталышынан '''''b'' '''векторунун аягына жүргүзүлгөн вектор '''<math>a</math>''' жана '''''b'' '''векторлорунун с у м м а с ы '''''<math>a</math>+b'' '''деп аталат (эгер '''''<math>a</math>'''''нын аягы м-н '''''b'''''нын башталышы дал келишсе). Векторлорду кошуунун төмөнкүдөй касиеттери бар: <math>a+b=b+a</math>(коммутативдик), '''<math>(a+b)+c=a+(b+c)</math>'''(ассоциативдик), <math>a+0=a</math> (нөлдүк элементтин болушу), <math>a+(-a)=0</math>(карама-каршы элементтин болушу), мында '''0 '''– нөлдүк вектор, <math>-a</math> вектору '''''<math>a</math>'' '''векторуна карама-каршы вектор. <math>x+b=a</math> барабардыгын канааттандырган '''''х'' '''вектору '''''<math>a</math>'' '''ж-а <math>b</math> векторлорунун <math>a-b</math> айырмасы деп аталат. Модулу <math>\left\vert \lambda \right\vert</math><math>\left\vert a \right\vert</math>болгон (эгер <math>\lambda>0</math> болсо, багыты <math>a</math>нын багытына дал келген жана <math>\lambda<0</math>жана багыты '''''<math>a</math>'''''нын багытына карама-каршы багытталган) вектор <math>a</math> <math>(a\neq0)</math> векторунун <math>\lambda(\lambda\neq0)</math>)санына болгон көбөйтүндүсү <math>\lambda</math><math>a</math> деп аталат. Эгер <math>\lambda=0</math> же (ж-а) <math>a=0</math> болсо, анда <math>\lambda</math><math>a=0</math> болот. Векторлорду санга көбөйтүү төмөнкү касиеттерге ээ: <math>\lambda(a+b)=\lambda</math><math>a</math><math>+</math><math>\lambda</math><math>b</math>(векторлорду кошууга карата дистрибутивдик), <math>(\lambda+\mu)a=\lambda</math><math>a</math><math>+</math><math>\mu</math><math>a</math> (сандарды кошууга карата дистрибутивдик), <math>\lambda</math>(<math>\mu</math>'''''<math>a</math>)'''''<math>=</math>'''''(<math>\lambda</math>'''''<math>\mu</math>''''')<math>a</math>'' '''(ассоциативдик), <math>1\cdot</math> <math>a=a</math>(1ге көбөйтүү). Мейкиндиктеги бардык векторлордун көптүгүн (киргизилген жана жогорудагы аксиомаларга баш ийген векторлорду кошуу жана санга көбөйтүү операциялары менен бирдикте) ''вектордук мейкиндик'' деп айтылат.<br/> | <br/>векторлор м-н жүргүзүлгөн эӊ жөнөкөй амалдарды окутуп-үйрөтүүчү ''вектордук эсептөөнүн'' бир бөлүмү. Алар векторлор м-н жүргүзүлгөн с ы з ы к т у у а м а л д а р: векторлорду кошуу ж-а векторду санга көбөйтүү. <math>a</math> векторунун башталышынан '''''b'' '''векторунун аягына жүргүзүлгөн вектор '''<math>a</math>''' жана '''''b'' '''векторлорунун с у м м а с ы '''''<math>a</math>+b'' '''деп аталат (эгер '''''<math>a</math>'''''нын аягы м-н '''''b'''''нын башталышы дал келишсе). Векторлорду кошуунун төмөнкүдөй касиеттери бар: <math>a+b=b+a</math>(коммутативдик), '''<math>(a+b)+c=a+(b+c)</math>'''(ассоциативдик), <math>a+0=a</math> (нөлдүк элементтин болушу), <math>a+(-a)=0</math>(карама-каршы элементтин болушу), мында '''0 '''– нөлдүк вектор, <math>-a</math> вектору '''''<math>a</math>'' '''векторуна карама-каршы вектор. <math>x+b=a</math> барабардыгын канааттандырган '''''х'' '''вектору '''''<math>a</math>'' '''ж-а <math>b</math> векторлорунун <math>a-b</math> айырмасы деп аталат. Модулу <math>\left\vert \lambda \right\vert</math><math>\left\vert a \right\vert</math>болгон (эгер <math>\lambda>0</math> болсо, багыты <math>a</math>нын багытына дал келген жана <math>\lambda<0</math>жана багыты '''''<math>a</math>'''''нын багытына карама-каршы багытталган) вектор <math>a</math> <math>(a\neq0)</math> векторунун <math>\lambda(\lambda\neq0)</math>)санына болгон көбөйтүндүсү <math>\lambda</math><math>a</math> деп аталат. Эгер <math>\lambda=0</math> же (ж-а) <math>a=0</math> болсо, анда <math>\lambda</math><math>a=0</math> болот. Векторлорду санга көбөйтүү төмөнкү касиеттерге ээ: <math>\lambda(a+b)=\lambda</math><math>a</math><math>+</math><math>\lambda</math><math>b</math>(векторлорду кошууга карата дистрибутивдик), <math>(\lambda+\mu)a=\lambda</math><math>a</math><math>+</math><math>\mu</math><math>a</math> (сандарды кошууга карата дистрибутивдик), <math>\lambda</math>(<math>\mu</math>'''''<math>a</math>)'''''<math>=</math>'''''(<math>\lambda</math>'''''<math>\mu</math>''''')<math>a</math>'' '''(ассоциативдик), <math>1\cdot</math> <math>a=a</math>(1ге көбөйтүү). Мейкиндиктеги бардык векторлордун көптүгүн (киргизилген жана жогорудагы аксиомаларга баш ийген векторлорду кошуу жана санга көбөйтүү операциялары менен бирдикте) ''вектордук мейкиндик'' деп айтылат.<br/> | ||
==Вектордук анализ, == | ==Вектордук анализ, == | ||
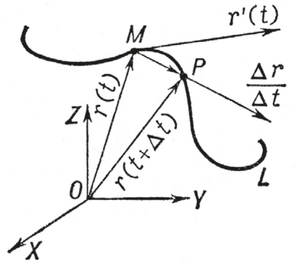
<br/>в е к т о р д у к т а л д о о – вектордук эсептөөлөрдүн бир бөлүмү. Ал вектордук ж-а скалярдык талааларды, векторлордун матем. касиеттерин үйрөтөт. Мында ''математикалык анализдин'' каражаттары менен бир же көп аргументтү вектордук жана скалярдык функциялар изилденет. Эгер <math>\{t\}</math> көптүгүндөгү <math>t</math> өзгөрмөсүнүн ар бир маанисине белгилүү бир закон б-ча r вектору туура келсе, анда <math>\{t\}</math> көптүгүндө <math>r = r (t)</math>вектор-функциясы берилген деп эсептелет. 3 өлчөмдүү мейкиндикте <math>r = r (t)</math> вектор- функциясынын берилиши ) <math>x = x(t), y = y(t), z = z(t)</math> үч скалярдык функциясынын берилишине эквиваленттүү. Координата башталышы – 0дөн чыккан <math>r(t)</math> векторлорунун учтарынын көптүгү г о д о г р а ф деп аталат. Эгер <math>t</math> аргументи убакыт катары алынса, анда <math>r(t)</math>вектор функциясы, <math>r(t)</math> функциясынын годографы L ийри сызыгынын М чекитиндеги кыймыл законун көрсөтөт. Вектор – функцияны үйрөтүүдө туунду түшүнүгү чоӊ роль аткарат ж-а төмөнкүчө киргизилет: эгер t аргументине <math>\Delta</math><math>t\neq0</math> өсүндүсү берилсе жана <math>\Delta r = r(t + \Delta t) - r(t)</math> вектору (сүрөттө МР вектору) <math>1/\Delta t</math>га көбөйтүлсө, анда <math>\Delta t \rightarrow 0</math> 0 болгондо <math>dr/dt</math> катышынын чеги (предели) <math>r(t)</math> вектор функциясынын т у у н д у с у деп аталат, ал <math>r(t)</math> же <math>dr/dt</math> аркылуу белгиленет. Бул туунду – L ийри сызыгынын (годографынын) М чекитинде жүргүзүлгөн жаныма. Эгер <math>r(t)</math> функциясы М чекитинин L ийри сызыгы боюнча чекиттин кыймыл закону деп каралса, анда <math>r(t)</math> туундусу ушул чекиттин кыймылынын ылдамдыгы болуп эсептелет. Вектор-функциялардын түрдү көбөйтүндүлөрүн эсептөө эрежелери кадимки функциялардыкына окшош: | <br/>в е к т о р д у к т а л д о о – вектордук эсептөөлөрдүн бир бөлүмү. Ал вектордук ж-а скалярдык талааларды, векторлордун матем. касиеттерин үйрөтөт. Мында ''математикалык анализдин'' каражаттары менен бир же көп аргументтү вектордук жана скалярдык функциялар изилденет. Эгер <math>\{t\}</math> көптүгүндөгү <math>t</math> өзгөрмөсүнүн ар бир маанисине белгилүү бир закон б-ча r вектору туура келсе, анда <math>\{t\}</math> көптүгүндө <math>r = r (t)</math>вектор-функциясы берилген деп эсептелет. 3 өлчөмдүү мейкиндикте <math>r = r (t)</math> вектор- функциясынын берилиши ) <math>x = x(t), y = y(t), z = z(t)</math> үч скалярдык функциясынын берилишине эквиваленттүү. Координата башталышы – 0дөн чыккан <math>r(t)</math> векторлорунун учтарынын көптүгү г о д о г р а ф деп аталат. Эгер <math>t</math> аргументи убакыт катары алынса, анда <math>r(t)</math>вектор функциясы, <math>r(t)</math> функциясынын годографы L ийри сызыгынын М чекитиндеги кыймыл законун көрсөтөт. Вектор – функцияны үйрөтүүдө туунду түшүнүгү чоӊ роль аткарат ж-а төмөнкүчө киргизилет: эгер t аргументине <math>\Delta</math><math>t\neq0</math> өсүндүсү берилсе жана <math>\Delta r = r(t + \Delta t) - r(t)</math> вектору (сүрөттө МР вектору) <math>1/\Delta t</math>га көбөйтүлсө, анда <math>\Delta t \rightarrow 0</math> 0 болгондо <math>dr/dt</math> катышынын чеги (предели) <math>r(t)</math> вектор функциясынын т у у н д у с у деп аталат, ал <math>r(t)</math> же <math>dr/dt</math> аркылуу белгиленет. Бул туунду – L ийри сызыгынын (годографынын) М чекитинде жүргүзүлгөн жаныма. Эгер <math>r(t)</math> функциясы М чекитинин L ийри сызыгы боюнча чекиттин кыймыл закону деп каралса, анда <math>r(t)</math> туундусу ушул чекиттин кыймылынын ылдамдыгы болуп эсептелет. Вектор-функциялардын түрдү көбөйтүндүлөрүн эсептөө эрежелери кадимки функциялардыкына окшош: <math>(r_1,r_2)'=(r_1 ' ,r_2\bigr)+(r_1,r'_2),[r_1,r_2]'=[r'_1,r_2]+[r_1,r'_2].</math> Скалярдык | ||
<br/> | <br/> | ||
[[File:ВЕКТОРДУК ЭСЕПТӨӨ –67.png | thumb | none]] | [[File:ВЕКТОРДУК ЭСЕПТӨӨ –67.png | thumb | none]] | ||
05:58, 28 Март (Жалган куран) 2025 -га соңку нускасы
ВЕКТОРДУК ЭСЕПТӨӨ – математиканын евклид мейкиндигиндеги векторлорду ж-а алар м-н болгон амалдарды изилдөөчү бөлүмү. В. э. 19-к-дын орто ченинен баштап механика ж-а физикада коюлган талаптарга жараша өнүккөн. Англ. математик У. Гамильтон ж-а нем. математиги Г. Грассмандын (1844–50) гиперкомплекстик сандарды изилдөөлөрү В. э-гө негиз салган. Алардын идеяларын англ. физик К. Максвелл электр ж-а магнит ж-дөгү эмгектеринде пайдаланган. Амер. физик Ж. Гиббс В. э-нү азыркы деӊгээлине жеткирген. В. э-нүн өсүшүнө орус математиктери М. В. Остроградский, А. П. Котельников ж-а сов. илимпоздор Д. Н. Зейлигер, П. А. Широков ж. б. чоӊ салым кошушкан. В. э. вектордук алгебра ж-а вектордук
анализ болуп бөлүнөт.
Вектордук алгебра –
векторлор м-н жүргүзүлгөн эӊ жөнөкөй амалдарды окутуп-үйрөтүүчү вектордук эсептөөнүн бир бөлүмү. Алар векторлор м-н жүргүзүлгөн с ы з ы к т у у а м а л д а р: векторлорду кошуу ж-а векторду санга көбөйтүү. векторунун башталышынан b векторунун аягына жүргүзүлгөн вектор жана b векторлорунун с у м м а с ы +b деп аталат (эгер нын аягы м-н bнын башталышы дал келишсе). Векторлорду кошуунун төмөнкүдөй касиеттери бар: (коммутативдик), (ассоциативдик), (нөлдүк элементтин болушу), (карама-каршы элементтин болушу), мында 0 – нөлдүк вектор, вектору векторуна карама-каршы вектор. барабардыгын канааттандырган х вектору ж-а векторлорунун айырмасы деп аталат. Модулу болгон (эгер болсо, багыты нын багытына дал келген жана жана багыты нын багытына карама-каршы багытталган) вектор векторунун )санына болгон көбөйтүндүсү деп аталат. Эгер же (ж-а) болсо, анда болот. Векторлорду санга көбөйтүү төмөнкү касиеттерге ээ: (векторлорду кошууга карата дистрибутивдик), (сандарды кошууга карата дистрибутивдик), ()() (ассоциативдик), (1ге көбөйтүү). Мейкиндиктеги бардык векторлордун көптүгүн (киргизилген жана жогорудагы аксиомаларга баш ийген векторлорду кошуу жана санга көбөйтүү операциялары менен бирдикте) вектордук мейкиндик деп айтылат.
Вектордук анализ,
в е к т о р д у к т а л д о о – вектордук эсептөөлөрдүн бир бөлүмү. Ал вектордук ж-а скалярдык талааларды, векторлордун матем. касиеттерин үйрөтөт. Мында математикалык анализдин каражаттары менен бир же көп аргументтү вектордук жана скалярдык функциялар изилденет. Эгер көптүгүндөгү өзгөрмөсүнүн ар бир маанисине белгилүү бир закон б-ча r вектору туура келсе, анда көптүгүндө вектор-функциясы берилген деп эсептелет. 3 өлчөмдүү мейкиндикте вектор- функциясынын берилиши ) үч скалярдык функциясынын берилишине эквиваленттүү. Координата башталышы – 0дөн чыккан векторлорунун учтарынын көптүгү г о д о г р а ф деп аталат. Эгер аргументи убакыт катары алынса, анда вектор функциясы, функциясынын годографы L ийри сызыгынын М чекитиндеги кыймыл законун көрсөтөт. Вектор – функцияны үйрөтүүдө туунду түшүнүгү чоӊ роль аткарат ж-а төмөнкүчө киргизилет: эгер t аргументине өсүндүсү берилсе жана вектору (сүрөттө МР вектору) га көбөйтүлсө, анда 0 болгондо катышынын чеги (предели) вектор функциясынын т у у н д у с у деп аталат, ал же аркылуу белгиленет. Бул туунду – L ийри сызыгынын (годографынын) М чекитинде жүргүзүлгөн жаныма. Эгер функциясы М чекитинин L ийри сызыгы боюнча чекиттин кыймыл закону деп каралса, анда туундусу ушул чекиттин кыймылынын ылдамдыгы болуп эсептелет. Вектор-функциялардын түрдү көбөйтүндүлөрүн эсептөө эрежелери кадимки функциялардыкына окшош: Скалярдык
талааны окуп-үйрөнүүнүн негизги түшүнүктөрүнүн бири болуп градиент эсептелет. Вектордук анализдин негизги дифференциалдык амалдары – градиент, дивергенция ж-а куюн (ротор). В. а-ди амер. физик Ж. Гиббс киргизген. Орус окумуштуусу М. В. Остроградский анын негизги теоремасын далилдеген. Англ. физик О. Хевисайд В. а-ди өз эмгектеринде 1882-жылдан тартып колдоно баштаган. 1907-ж. орус математиги П. О. Сомовдун «Вектордук анализ» деген китеби жарык көргөн.
Ад.: Александров П. С. Лекции по аналитической геометрии. М., 1968; Ефимов Н. В. Краткий курс аналитической геометрии. 9-ое изд. М., 1967.
А. А. Чекеев, С. С. Токсонбаев.




































![{\displaystyle (r_{1},r_{2})'=(r_{1}',r_{2}{\bigr )}+(r_{1},r'_{2}),[r_{1},r_{2}]'=[r'_{1},r_{2}]+[r_{1},r'_{2}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ccf8d74ab350489c2024f0a00af6dde1d2eb2b5)