БУРАЛМА БЕТ: нускалардын айырмасы
Навигацияга өтүү
Издөөгө өтүү
м (1 версия) |
No edit summary |
||
| 1 сап: | 1 сап: | ||
'''БУРАЛМА БЕТ''' , г е л и к о и д – ОО’ кыймылсыз октун айланасында турактуу бурчтук ылдамдык | '''БУРАЛМА БЕТ''' , г е л и к о и д – ОО’ кыймылсыз октун айланасында турактуу бурчтук ылдамдык менен айлангандагы жана бир эле убакта ошол окту бойлой алга жылуудагы L ийри сызыгы менен сүрөттөлгөн бет (1-сүрөт). <br/> | ||
<br/> | |||
[[File:БУРАЛМА БЕТ19.png | thumb | none]] | [[File:БУРАЛМА БЕТ19.png | thumb | none]] | ||
[[File:БУРАЛМА БЕТ20.png | thumb | none]] | [[File:БУРАЛМА БЕТ20.png | thumb | none]] | ||
1-сүрөт. 2-сүрөт. | 1-сүрөт. 2-сүрөт.<br/>Эгер ''L'' ийри сызыгы айлануу огунун тегиздигинде жатса ж-а ''z=f(u'') теӊдемеси менен аныкталса, анда Буралма беттин радиус-вектору:<br/>''r={u''cos'', u''sin'', f(u)+h()}, h''=con''st,'' ал эми анын сызыктуу элементи: ''ds''<sup>2</sup>=(1+''f '''<sup>2</sup>)''du''<sup>2</sup>+2''hf ' dud + (u''<sup>2</sup>+''h''<sup>2</sup>)''d''<sup>2</sup> болот. Эгер ''f=const'', башкача айтканда Буралма бет түз сызык менен сүрөттөлсө, анда ал г е л и к о и д деп аталат (2-сүрөт). Эгер ''h''=0 болсо, анда Буралма бет айлануу бети деп аталат. | ||
<br/>Эгер ''L'' ийри сызыгы айлануу огунун тегиздигинде жатса ж-а ''z=f(u'') теӊдемеси | |||
<br/>''r={u''cos'', u''sin'', f(u)+h()}, h''=con''st,'' ал эми анын сызыктуу элементи: ''ds''<sup>2</sup>=(1+''f '''<sup>2</sup>)''du''<sup>2</sup>+2''hf ' dud + (u''<sup>2</sup>+''h''<sup>2</sup>)''d''<sup>2</sup> болот. Эгер ''f=const'', | |||
[[Category: 2-том]] | [[Category: 2-том]] | ||
02:24, 14 Май (Бугу) 2024 -деги абалы
БУРАЛМА БЕТ , г е л и к о и д – ОО’ кыймылсыз октун айланасында турактуу бурчтук ылдамдык менен айлангандагы жана бир эле убакта ошол окту бойлой алга жылуудагы L ийри сызыгы менен сүрөттөлгөн бет (1-сүрөт).
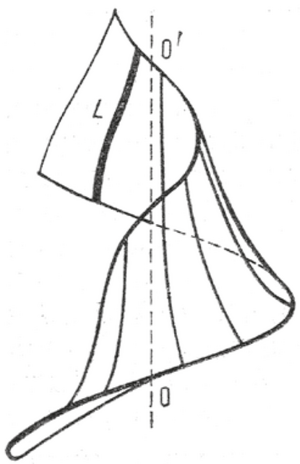
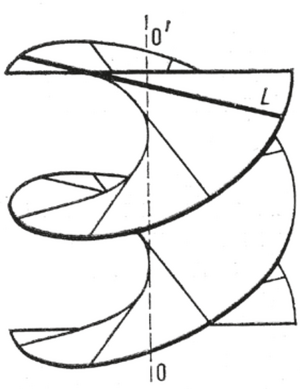
1-сүрөт. 2-сүрөт.
Эгер L ийри сызыгы айлануу огунун тегиздигинде жатса ж-а z=f(u) теӊдемеси менен аныкталса, анда Буралма беттин радиус-вектору:
r={ucos, usin, f(u)+h()}, h=const, ал эми анын сызыктуу элементи: ds2=(1+f '2)du2+2hf ' dud + (u2+h2)d2 болот. Эгер f=const, башкача айтканда Буралма бет түз сызык менен сүрөттөлсө, анда ал г е л и к о и д деп аталат (2-сүрөт). Эгер h=0 болсо, анда Буралма бет айлануу бети деп аталат.