ДИФФЕРЕНЦИАЛ ЭСЕПТӨӨЛӨРҮ

ДИФФЕРЕНЦИА́Л ЭСЕПТӨӨЛӨРҮ – математи­канын функция туундулары м-н дифференциал­дарын эсептөөчү ж-а алар аркылуу функциянын касиетин изилдөөчү бөлүмү. Д. э. интеграл эсеп­төөлөрү м-н тыгыз байланышта ж-а аны м-н биригип, математикалык анализдин негизин түзөт. Д. э-нүн өнүгүшү математикага өзгөрмө чоңдук түшүнүгүн киргизген Р. Декарттын, дифференциал ж-а интеграл эсептөөлөрдүн не­гизин түзүшкөн И. Ньютон м-н Г. Лейбниц­тин, Я. ж-а И. Бернуллилердин, Л. Эйлердин, предел түшүнүгү аркылуу матем. анализди теор. негиздеген О. Кошинин эмгектерине байла­ныштуу. Д. э. – математиканын эң маанилүү түшүнүктөрү – чыныгы сан, функция, предел ж-а үзгүлтүксүздүк түшүнүктөрүнө негизделген. Д. э. туунду ж-а дифференциал ж-дөгү негизги түшүнүктөргө таянып, функциялардын эң чоң ж-а эң кичине маанилерин табуу, ийри сызык­ка жаныма жүргүзүү, кыймылдын ылдамды­гын эсептөө маселелерин изилдейт.

Т у у н д у.

у= f(х) функциясынын х чекитиндеги өсүндү­сүнүн аргументтин өсүндүсүнө болгон катышы­нын ∆х нөлгө умтулгандагы предели функция­нын ушул чекиттеги туундусу деп аталып, у, f′(х₀), dу , dх df(х0 ) dх м-н белгиленет. Анда f¹(х )=

= lim ^∆у . Эгер ∆х→0 ∆х f′(х₀) чектүү болсо, анда f(х) функциясы х₀ чекитин-

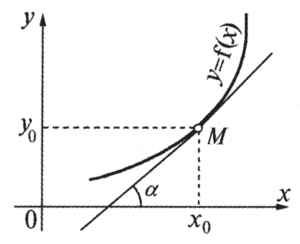
де дифференциял­дануучу деп ата­лат. Функция кан­дай дыр б ир ара­лыктын ар бир чекитинде дифференциялдануу­чу болсо, анда ал аралыкта да дифференциял­дануучу болот. Туундуну табуу амалы диффе­ренциалдоо деп аталат. Д. э-н геометрияга кол­донуу өтө маанилүү, жаныманын бурчтук коэфф-и, б. а. Ох огу м-н М(х₀; у₀) чекиттеги

у=f(х) ийри сызыгын жаныманын арасындагы α бурчунун тангенси (к. чийме) туундунун х=х₀ маанисине, б. а. f′(х₀)ке барабар. Механикада туундуну түз сызыктуу кыймылдагы чекиттин _d2 ылдамдыгы катары кароого болот. Д. э. инте­грал эсептөөлөрүндөй эле көп колдонулат. Ж. Асанова.